Getting Started With Proportional Control On A Micromelon Rover

BACK TO POSTS

Have you ever wondered how automatic sprinklers work? How autopilot on a plane works? How cars can automatically keep their speed using cruise control? These robots or systems are controlled by something called a “control system”.

Imagine you have a beautiful garden bed with different vegetables you’re trying to grow. You could use a proportional controller for a sprinkler system to ensure that the plants are getting exactly as much water as they need all year long. It’ll even handle rainy or dry seasons just fine. How would that work?

Proportional control means that you are controlling something in relation to something. In this case, we would want to control moisture in the soil in relation to the water needs of our plant. We could even use the exact same controller for two different vegetable plants needing completely different amounts of water by scaling the exact same system up or down.

Okay, so control systems sound pretty cool, how does something like that actually work?

Let’s say we have our garden installed with a sprinkler system. The sprinkler system is our output and the thing we are controlling is the amount of water they put into our soil.

We need something called an input. The most obvious here is likely a moisture sensor in the soil near the roots of our plant. Let’s suppose this device tells us exactly how much water is in the soil as an input into our control system.

We also have something called a “goal” or a “target”. This is the outcome we are trying to achieve and the result we are constantly striving for. In this case that’s how much water our plant needs.

All a proportional controller does is increase or decrease our output (water coming out of our sprinklers) proportional to how far off of our goal we are.(how thirsty or drowned our plants are at any given time based on the moisture sensor reading)

You could in this example consider the difference in moisture from the ground to what the plant needs to be our “error”, and one more piece of our control system recipe is our proportional gain, commonly denoted as “Kp”. This is a simple multiplier that gets applied to our entire system, so that we can apply the same control system on a thirstier plant like cucumber with a Kp of something like 2 (meaning we double the water outputs) and reduce the water outputs with a kp of 0.5 if we are growing a cactus (meaning we halve the water outputs)

Control systems are so popular because this will deal with changes in circumstances and automates a lot of the work that would go into managing this garden. Did it rain last night? Moisture sensor will give the input that we have a lot of water in the soil, and will appropriately limit or turn off the sprinkler system because it has recognised it already has plenty of water. Has it been a particularly hot day? Moisture sensor will let the system know the ground is drier than usual and the sprinklers can be programmed to stay on for longer, all of which can be scaled for different plants using our Kp values for different water requirements.
Less people would be required to manage a larger garden if a control system can ensure people don’t have to spend time worrying about these things.

It is this incredible versatility of the control system setup that allows us to use it in many applications from garden beds to micromelon robots. For our robot we could vary our speed based on sensor inputs.

Recap of Control System Components:

The goal which is the target

The Inputs which is all the information the control loop is given. (e.g. soil moisture, car speed, plane altitude, etc.)

The output which is the result of the changes your control system made, and the thing you are trying to get close to your goal, or increase towards your goal. (e.g. time on for sprinklers, more gas for car, turning up the plane throttle, etc.)

An error, which is a measure of how far away your system currently is from your goal or desired behaviour.

Gain, usually simply a value denoted as “K” or in the context of proportional control “Kp” which scales how drastically your system reacts to your error.

Control System Elements:

A classical example of a control system is the cruise control in a car. Let’s dive into what some of the previous terminology would look like in the context of cruise control as another example:

Goal:

In cruise control, your goal is for the car to remain at the speed you have specified. Let’s make our goal a speed of 80km/h.

However, there are many things that will disrupt this speed. Friction of the road, changing air resistance due to wind/car speed, etc. There is too much going on to easily model this car using only physics.

Error:

Let’s say the car drops to a speed of 75km/h due to aforementioned effects. The control system first calculates an error based on its inputs, which in this case would be the speedometer telling the control system the current speed of 75km/h. It could in this case simply compute 80-75km/h means that we have an error of 5km/h and our goal becomes to make this error as small as possible. The obvious answer here is to accelerate the car, but the question becomes: How much acceleration do we need?

Gain (Kp):

This is where we can use our Kp value to define exactly how drastically our system should respond to this error. A Kp value that is too high will result in the cruise controller to add an unreasonable amount of gas usage, meaning we will almost certainly greatly overshoot our goal of 80km/h, at which point we suddenly need to use the brakes to get back to our goal, but with a Kp too high we will likely slow down too much because our responses are too drastic and it will take a while before we finally get to our goal. A Kp too small may not be suitable either. If the Kp increases the gas by too little, we may only be able to reach a speed of 77km/h because the system will not make a change that is great enough for us to reach 80km/h.

Figure 1: System response of a high Kp vs a low Kp

Proportional Control Applications With a Micromelon Rover

By now we’ve seen an application with cruise control, but you could control almost any action the robot does based on any of the available inputs. You could vary the speed of the rover’s wheels based on its colour sensors, ultrasonic sensors, gyro sensor, etc. You could even combine multiple inputs and have them control one or multiple outputs.
Let’s do a very simple example first of changing speed based on ultrasonic sensor distance.

Figure 2: Simple proportional control example

This very small snippet of code essentially behaves like a proportional controller, and is likely the most simple one you can make.

Input and Output: Your input is the ultrasonic sensor distance value that the rover currently sees. Our output is the rover’s wheel speed.

Goal: Match the rover’s speed to the live ultrasonic sensor distance

Error: Our error is less obvious. If our rover is 10cm away from a wall, and we move straight towards it at 10cm/s, that means if we move forwards for 0.1 seconds our ultrasonic distance will read 9. Our error is that we used to be moving at 10cm/s, but our input tells us that now to achieve our goal of matching the speed and the distance, our error is 1cm/s (10cm/s - 9cm distance) and the system dynamically adjusts for this instantly by just setting the outputs (motor speed) to our ultrasonic distance achieving our goal very efficiently.

Kp: This program does not have a Kp, so it can be thought of as 1 as we are not scaling our speed based on our distance in this example just yet. If we wanted to move at half the speed of our ultrasonic sensor, then instead of simply inserting the ultrasonic sensor distance, we could do 0.5 * ultrasonic distance, meaning our Kp is 0.5.

Figure 3: Example showing implementation of Kp = 0.5

This is also largely because we have changed our goal along with our Kp value. The goal is to now move at half of our sensor distance.

This is a very simplistic and not very intelligent example.However, let’s now generalise our program so that we can easily change our goal and stop a certain distance away from our goal. The Micromelon IDE has a code example of a PID controller (in the advanced section) which is a much more complex version of a Proportional controller.

The proportional version does not control the rover as smoothly as the more complex PID example, but it is a nice demonstration of the things we have discussed so far.
Proportional control is used in a PID controller to dictate in this case how much speed is required, whereas the integral (I) and derivative (D) terms are to prevent the system from overreacting to an error spike or overshooting the goal.

This example also shows a lot more intelligent defensive programming. This means that it accounts for situations where our controller values may get far outside of what we need and it’s good practice to think critically about the ways your system may spin out of control.

Let’s Break It Down:

For these first two blocks we can define how far away from objects we’d like to stop, and what our Kp gain value is. Experiment with different Kp values and observe what happens! (e.g. 0.1 and 10)

We set up an infinite while true loop so that the code goes on forever until stopped by the user. (Note: It is technically not great practice to have an infinite while loop, but for the sake of this example it will do) The first thing we need to do at the start of our loop is receive the data from our sensors and define that as our distance reading called “dist”. Based on this distance, we can find out how large our error is by subtracting it off our current distance. (e.g. if our goal is 10 cm and our sensor says we are 23 cm away from the wall, our dist is 23 and error is 23-10=13)

This is some defensive programming. We want our difference values to fall between the numbers 0 and 30, whereas the Ultrasonic Sensor can produce values from 0 - 255. We just want to ensure that values don’t spiral out of control and the robot tries to move at 100cm/s.

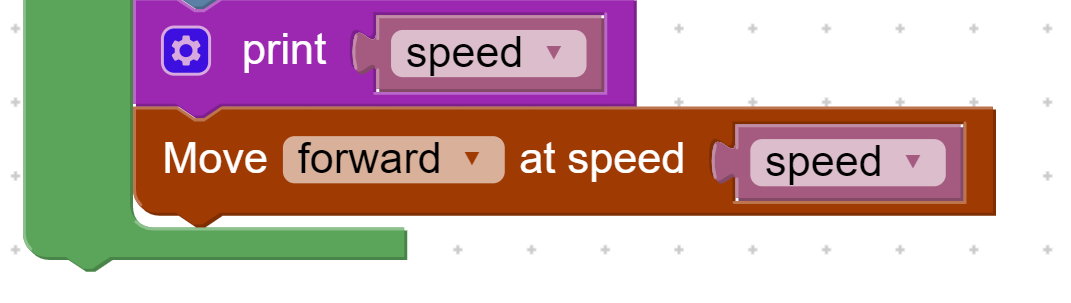
This is where we adjust our speed similar to our previous example. We set our motor speed to be our error between our goal and current sensor reading (the 13 value from before)

If a high Kp value shoots up our speed value far above 30 or -30 again, that’s the top speed of our robot! That means we need to restrict the values. The program can do this automatically, but it’s better to have it in your code as defensive programming.

Finally, we print the speed so that we can see it in our console, and we make the rover move at the speed we have calculated using our controller.

Limitations of Proportional Control

Proportional controllers are only the beginning! They are quite simple in comparison to the many other types of controllers out there. Some control problems can’t be solved by proportional control, and most are simply more effective and efficient with more intelligent controllers. A car's cruise control or a plane’s autopilot will have much more complex systems in place to make a more effective and efficient solution.

Proportional controllers unfortunately do have a tendency to overshoot their goal. Unless you are okay with getting to your goal very slowly, proportional control can only do so much. It’s a system that will get you to your destination, but it is quite bad at slowing down before it gets to its goal.

Proportional controllers are also not very good at dealing with imperfect data or inaccurate sensor readings. The point of a PID controller (Proportional, Integral and Derivative) is that the integral and derivative terms dampen and smooth out errors so that your system does not overreact. It also means that if your sensor is inaccurate, it can average out the inaccuracies and hopefully arrive closer to the desired goal.

For more precise applications you can sometimes encounter something called a persistent error. This means that while the error usually decreases slightly over time it has a really difficult time getting the error down effectively once it’s close to the target. I foreshadowed this when in my cruise control example reaching only 77km/h instead of 80. In this case it’s possible for a controller designed with a low gain to have the extra gas applied at 77km/h to be too low for the car to speed up. A persistent error of 3km/h might be okay in some situations, but with a better controller you could stay at near perfect 80km/h.

Exercises Using Proportional Control:

While a lot of our exercises can be done without the use of a proportional controller, quite a few of them could be actually solved by such a system as a very reliable and dynamic solution. Here are just a few examples.

Balance Bot:

You can use a Proportional controller to balance on a seesaw. Your input is the accelerometer, your goal is to have 1g going downwards, and your error to minimise would be the difference between your accelerometer reading and 1g. See if you can adapt these concepts and try solving it for a more dynamic solution!

Driving School:

Did you know that the black road in this simulator activity is actually a slight gradient? The middle of the road is the darkest, and the outside of the road is lighter. You could use proportional control on the colour sensors to stay perfectly in the middle of the road! Your inputs are the left and right colour sensors, your goal is to make those two sensor values equal, and your error would be the difference between left and right sensor brightness. Try and stay in the middle of the road without touching the edges!

Line Following:

When a rover moves over a line, often only part of the sensor will cover the black line and part of it will still be on white. This means that while doing line following, the sensor outputs are more of a gradient than they adhere to a clear-cut threshold like the activity describes. You could use Proportional control with this gradient to make your line following much smoother. Your inputs would be the colour sensors, your error would be the difference between the left and right sensor to determine where the line is, and your goal is to minimise the difference between these two sensors. (minimise the error!) See if you can create a better line follower!